Invertible knot

In mathematics, especially in the area of topology known as knot theory, an invertible knot is a knot that can be continuously deformed to itself, but with its orientation reversed. A non-invertible knot is any knot which does not have this property. The invertibility of a knot is a knot invariant. An invertible link is the link equivalent of an invertible knot.

There are only five knot symmetry types, indicated by chirality and invertibility: fully chiral, reversible, positively amphichiral noninvertible, negatively amphichiral noninvertible, and fully amphichiral invertible.

Background

It has long been known that most of the simple knots, such as the trefoil knot and the figure-eight knot are invertible. In 1962 Ralph Fox conjectured that some knots were non-invertible, but it was not proved that non-invertible knots exist until Hale Trotter discovered an infinite family of pretzel knots that were non-invertible in 1963. It is now known almost all knots are non-invertible.

Invertible knots

The simplest non-trivial invertible knot, the trefoil knot. Rotating the knot 180 degrees in 3-space about an axis in the plane of the diagram produces the same knot diagram, but with the arrow's direction reversed.

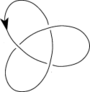
All knots with crossing number of 7 or less are known to be invertible. No general method is known that can distinguish if a given knot is invertible. The problem can be translated into algebraic terms, but unfortunately there is no known algorithm to solve this algebraic problem.

If a knot is invertible and amphichiral, it is fully amphichiral. The simplest knot with this property is the figure eight knot. A chiral knot that is invertible is classified as a reversible knot.

Strongly invertible knots

A more abstract way to define an invertible knot is to say there is an orientation-preserving homeomorphism of the 3-sphere which takes the knot to itself but reverses the orientation along the knot. By imposing the stronger condition that the homeomorphism also be an involution, i.e. have period 2 in the homeomorphism group of the 3-sphere, we arrive at the definition of a strongly invertible knot. All knots with tunnel number one, such as the trefoil knot and figure-eight knot, are strongly invertible.

Non-invertible knots

The non-invertible knot 8₁₇, the simplest of the non-invertible knots.

The simplest example of a non-invertible knot is the knot 8₁₇ (Alexander-Briggs notation) or .2.2 (Conway notation). The pretzel knot 7, 5, 3 is non-invertible, as are all pretzel knots of the form (2p + 1), (2q + 1), (2r + 1), where p, q, and r are distinct integers, which is the infinite family proven to be non-invertible by Trotter.

See also

• Chiral knot

External links

• Jablan, Slavik & Sazdanovic, Radmila. Basic graph theory: Non-invertible knot and links Archived 2011-01-18 at the Wayback Machine, LinKnot.
• Explanation with a video, Nrich.Maths.org.