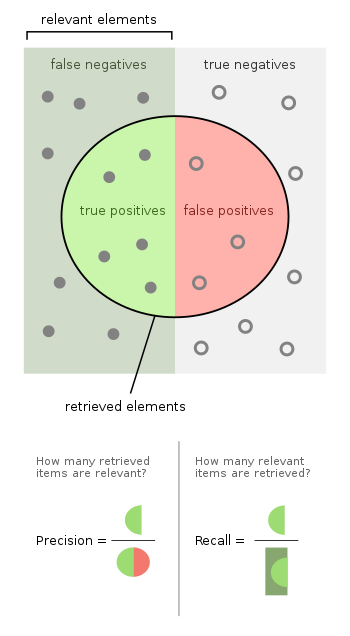
Precision and recall

Precision and recall

In pattern recognition, information retrieval, object detection and classification (machine learning), precision and recall are performance metrics that apply to data retrieved from a collection, corpus or sample space.

Precision (also called positive predictive value) is the fraction of relevant instances among the retrieved instances, while recall (also known as sensitivity) is the fraction of relevant instances that were retrieved. Both precision and recall are therefore based on relevance.

Consider a computer program for recognizing dogs (the relevant element) in a digital photograph. Upon processing a picture which contains ten cats and twelve dogs, the program identifies eight dogs. Of the eight elements identified as dogs, only five actually are dogs (true positives), while the other three are cats (false positives). Seven dogs were missed (false negatives), and seven cats were correctly excluded (true negatives). The program's precision is then 5/8 (true positives / selected elements) while its recall is 5/12 (true positives / relevant elements).

When a search engine returns 30 pages, only 20 of which are relevant, while failing to return 40 additional relevant pages, its precision is 20/30 = 2/3, which tells us how valid the results are, while its recall is 20/60 = 1/3, which tells us how complete the results are.

Adopting a hypothesis-testing approach from statistics, in which, in this case, the null hypothesis is that a given item is irrelevant (i.e., not a dog), absence of type I and type II errors (i.e., perfect specificity and sensitivity of 100% each) corresponds respectively to perfect precision (no false positive) and perfect recall (no false negative).

More generally, recall is simply the complement of the type II error rate (i.e., one minus the type II error rate). Precision is related to the type I error rate, but in a slightly more complicated way, as it also depends upon the prior distribution of seeing a relevant vs. an irrelevant item.

The above cat and dog example contained 8 − 5 = 3 type I errors (false positives) out of 10 total cats (true negatives), for a type I error rate of 3/10, and 12 − 5 = 7 type II errors, for a type II error rate of 7/12. Precision can be seen as a measure of quality, and recall as a measure of quantity. Higher precision means that an algorithm returns more relevant results than irrelevant ones, and high recall means that an algorithm returns most of the relevant results (whether or not irrelevant ones are also returned).

Introduction

In information retrieval, the instances are documents and the task is to return a set of relevant documents given a search term. Recall is the number of relevant documents retrieved by a search divided by the total number of existing relevant documents, while precision is the number of relevant documents retrieved by a search divided by the total number of documents retrieved by that search.

In a classification task, the precision for a class is the number of true positives (i.e. the number of items correctly labelled as belonging to the positive class) divided by the total number of elements labelled as belonging to the positive class (i.e. the sum of true positives and false positives, which are items incorrectly labelled as belonging to the class). Recall in this context is defined as the number of true positives divided by the total number of elements that actually belong to the positive class (i.e. the sum of true positives and false negatives, which are items which were not labelled as belonging to the positive class but should have been).

In information retrieval, a perfect precision score of 1.0 means that every result retrieved by a search was relevant (but says nothing about whether all relevant documents were retrieved) whereas a perfect recall score of 1.0 means that all relevant documents were retrieved by the search (but says nothing about how many irrelevant documents were also retrieved).

Precision and recall are not particularly useful metrics when used in isolation. For instance, it is possible to have perfect recall by simply retrieving every single item. Likewise, it is possible to have near-perfect precision by selecting only a very small number of extremely likely items.

In a classification task, a precision score of 1.0 for a class C means that every item labelled as belonging to class C does indeed belong to class C (but says nothing about the number of items from class C that were not labelled correctly) whereas a recall of 1.0 means that every item from class C was labelled as belonging to class C (but says nothing about how many items from other classes were incorrectly also labelled as belonging to class C).

Often, there is an inverse relationship between precision and recall, where it is possible to increase one at the cost of reducing the other. Brain surgery provides an illustrative example of the tradeoff. Consider a brain surgeon removing a cancerous tumor from a patient's brain. The surgeon needs to remove all of the tumor cells since any remaining cancer cells will regenerate the tumor. Conversely, the surgeon must not remove healthy brain cells since that would leave the patient with impaired brain function. The surgeon may be more liberal in the area of the brain he removes to ensure he has extracted all the cancer cells. This decision increases recall but reduces precision. On the other hand, the surgeon may be more conservative in the brain cells he removes to ensure he extracts only cancer cells. This decision increases precision but reduces recall. That is to say, greater recall increases the chances of removing healthy cells (negative outcome) and increases the chances of removing all cancer cells (positive outcome). Greater precision decreases the chances of removing healthy cells (positive outcome) but also decreases the chances of removing all cancer cells (negative outcome).

Usually, precision and recall scores are not discussed in isolation. Instead, either values for one measure are compared for a fixed level at the other measure (e.g. precision at a recall level of 0.75) or both are combined into a single measure. Examples of measures that are a combination of precision and recall are the F-measure (the weighted harmonic mean of precision and recall), or the Matthews correlation coefficient, which is a geometric mean of the chance-corrected variants: the regression coefficients Informedness (DeltaP') and Markedness (DeltaP).Accuracy is a weighted arithmetic mean of Precision and Inverse Precision (weighted by Bias) as well as a weighted arithmetic mean of Recall and Inverse Recall (weighted by Prevalence). Inverse Precision and Inverse Recall are simply the Precision and Recall of the inverse problem where positive and negative labels are exchanged (for both real classes and prediction labels). Recall and Inverse Recall, or equivalently true positive rate and false positive rate, are frequently plotted against each other as ROC curves and provide a principled mechanism to explore operating point tradeoffs. Outside of Information Retrieval, the application of Recall, Precision and F-measure are argued to be flawed as they ignore the true negative cell of the contingency table, and they are easily manipulated by biasing the predictions. The first problem is 'solved' by using Accuracy and the second problem is 'solved' by discounting the chance component and renormalizing to Cohen's kappa, but this no longer affords the opportunity to explore tradeoffs graphically. However, Informedness and Markedness are Kappa-like renormalizations of Recall and Precision, and their geometric mean Matthews correlation coefficient thus acts like a debiased F-measure.

Definition (information retrieval context)

In information retrieval contexts, precision and recall are defined in terms of a set of retrieved documents (e.g. the list of documents produced by a web search engine for a query) and a set of relevant documents (e.g. the list of all documents on the internet that are relevant for a certain topic), cf. relevance.

Precision

In the field of information retrieval, precision is the fraction of retrieved documents that are relevant to the query:

$${\displaystyle {\text{precision}}={\frac {|\{{\text{relevant documents}}\}\cap \{{\text{retrieved documents}}\}|}{|\{{\text{retrieved documents}}\}|}}}$$

For example, for a text search on a set of documents, precision is the number of correct results divided by the number of all returned results.

Precision takes all retrieved documents into account, but it can also be evaluated at a given cut-off rank, considering only the topmost results returned by the system. This measure is called precision at n or P@n.

Precision is used with recall, the percent of all relevant documents that is returned by the search. The two measures are sometimes used together in the F₁ Score (or f-measure) to provide a single measurement for a system.

Note that the meaning and usage of "precision" in the field of information retrieval differs from the definition of accuracy and precision within other branches of science and technology.

Recall

In information retrieval, recall is the fraction of the relevant documents that are successfully retrieved.

$${\displaystyle {\text{recall}}={\frac {|\{{\text{relevant documents}}\}\cap \{{\text{retrieved documents}}\}|}{|\{{\text{relevant documents}}\}|}}}$$

For example, for a text search on a set of documents, recall is the number of correct results divided by the number of results that should have been returned.

In binary classification, recall is called sensitivity. It can be viewed as the probability that a relevant document is retrieved by the query.

Connection

Precision and recall can be interpreted as (estimated) conditional probabilities: Precision is given by ${\displaystyle P(C=P|{\hat {C}}=P)}$ while recall is given by ${\displaystyle P({\hat {C}}=P|C=P)}$, where ${\displaystyle {\hat {C}}}$ is the predicted class and ${\displaystyle C}$ is the actual class. Both quantities are, therefore, connected by Bayes' theorem.

Definition (classification context)

For classification tasks, the terms true positives, true negatives, false positives, and false negatives (see Type I and type II errors for definitions) compare the results of the classifier under test with trusted external judgments. The terms positive and negative refer to the classifier's prediction (sometimes known as the expectation), and the terms true and false refer to whether that prediction corresponds to the external judgment (sometimes known as the observation).

Let us define an experiment from P positive instances and N negative instances for some condition. The four outcomes can be formulated in a 2×2 contingency table or confusion matrix, as follows:

		Predicted condition		Sources: view talk edit
	Total population = P + N	Positive (PP)	Negative (PN)	Informedness, bookmaker informedness (BM) = TPR + TNR − 1	Prevalence threshold (PT) =${\displaystyle {\mathsf {\tfrac {{\sqrt {{\text{TPR}}\times {\text{FPR}}}}-{\text{FPR}}}{{\text{TPR}}-{\text{FPR}}}}}}$
Actual condition	Positive (P)	True positive (TP), hit	False negative (FN), type II error, miss, underestimation	True positive rate (TPR), recall, sensitivity (SEN), probability of detection, hit rate, power = TP/P = 1 − FNR	False negative rate (FNR), miss rate = FN/P = 1 − TPR
	Negative (N)	False positive (FP), type I error, false alarm, overestimation	True negative (TN), correct rejection	False positive rate (FPR), probability of false alarm, fall-out = FP/N = 1 − TNR	True negative rate (TNR), specificity (SPC), selectivity = TN/N = 1 − FPR
	Prevalence = P/P + N	Positive predictive value (PPV), precision = TP/PP = 1 − FDR	False omission rate (FOR) = FN/PN = 1 − NPV	Positive likelihood ratio (LR+) = TPR/FPR	Negative likelihood ratio (LR−) = FNR/TNR
	Accuracy (ACC) = TP + TN/P + N	False discovery rate (FDR) = FP/PP = 1 − PPV	Negative predictive value (NPV) = TN/PN = 1 − FOR	Markedness (MK), deltaP (Δp) = PPV + NPV − 1	Diagnostic odds ratio (DOR) = LR+/LR−
	Balanced accuracy (BA) = TPR + TNR/2	F1 score = 2 PPV × TPR/PPV + TPR = 2 TP/2 TP + FP + FN	Fowlkes–Mallows index (FM) = ${\displaystyle \scriptstyle {\mathsf {\sqrt {{\text{PPV}}\times {\text{TPR}}}}}}$	Matthews correlation coefficient (MCC) =${\displaystyle \scriptstyle {\mathsf {\sqrt {{\text{TPR}}\times {\text{TNR}}\times {\text{PPV}}\times {\text{NPV}}}}}}$${\displaystyle \scriptstyle -{\mathsf {\sqrt {{\text{FNR}}\times {\text{FPR}}\times {\text{FOR}}\times {\text{FDR}}}}}}$	Threat score (TS), critical success index (CSI), Jaccard index = TP/TP + FN + FP

Precision and recall are then defined as:

$${\displaystyle {\begin{aligned}{\text{Precision}}&={\frac {tp}{tp+fp}}\\{\text{Recall}}&={\frac {tp}{tp+fn}}\,\end{aligned}}}$$

Recall in this context is also referred to as the true positive rate or sensitivity, and precision is also referred to as positive predictive value (PPV); other related measures used in classification include true negative rate and accuracy. True negative rate is also called specificity.

$${\displaystyle {\text{True negative rate}}={\frac {tn}{tn+fp}}\,}$$

Imbalanced data

$${\displaystyle {\text{Accuracy}}={\frac {TP+TN}{TP+TN+FP+FN}}\,}$$

Accuracy can be a misleading metric for imbalanced data sets. Consider a sample with 95 negative and 5 positive values. Classifying all values as negative in this case gives 0.95 accuracy score. There are many metrics that don't suffer from this problem. For example, balanced accuracy (bACC) normalizes true positive and true negative predictions by the number of positive and negative samples, respectively, and divides their sum by two:

$${\displaystyle {\text{Balanced accuracy}}={\frac {TPR+TNR}{2}}\,}$$

For the previous example (95 negative and 5 positive samples), classifying all as negative gives 0.5 balanced accuracy score (the maximum bACC score is one), which is equivalent to the expected value of a random guess in a balanced data set. Balanced accuracy can serve as an overall performance metric for a model, whether or not the true labels are imbalanced in the data, assuming the cost of FN is the same as FP.

Another metric is the predicted positive condition rate (PPCR), which identifies the percentage of the total population that is flagged. For example, for a search engine that returns 30 results (retrieved documents) out of 1,000,000 documents, the PPCR is 0.003%.

$${\displaystyle {\text{Predicted positive condition rate}}={\frac {TP+FP}{TP+FP+TN+FN}}\,}$$

According to Saito and Rehmsmeier, precision-recall plots are more informative than ROC plots when evaluating binary classifiers on imbalanced data. In such scenarios, ROC plots may be visually deceptive with respect to conclusions about the reliability of classification performance.

Different from the above approaches, if an imbalance scaling is applied directly by weighting the confusion matrix elements, the standard metrics definitions still apply even in the case of imbalanced datasets. The weighting procedure relates the confusion matrix elements to the support set of each considered class.

Probabilistic interpretation

One can also interpret precision and recall not as ratios but as estimations of probabilities:

• Precision is the estimated probability that a document randomly selected from the pool of retrieved documents is relevant.
• Recall is the estimated probability that a document randomly selected from the pool of relevant documents is retrieved.

Another interpretation is that precision is the average probability of relevant retrieval and recall is the average probability of complete retrieval averaged over multiple retrieval queries.

F-measure

A measure that combines precision and recall is the harmonic mean of precision and recall, the traditional F-measure or balanced F-score:

$${\displaystyle F=2\cdot {\frac {\mathrm {precision} \cdot \mathrm {recall} }{\mathrm {precision} +\mathrm {recall} }}}$$

This measure is approximately the average of the two when they are close, and is more generally the harmonic mean, which, for the case of two numbers, coincides with the square of the geometric mean divided by the arithmetic mean. There are several reasons that the F-score can be criticized in particular circumstances due to its bias as an evaluation metric. This is also known as the ${\displaystyle F_{1}}$ measure, because recall and precision are evenly weighted.

It is a special case of the general ${\displaystyle F_{\beta }}$ measure (for non-negative real values of ${\displaystyle \beta }$):

$${\displaystyle F_{\beta }=(1+\beta ^{2})\cdot {\frac {\mathrm {precision} \cdot \mathrm {recall} }{\beta ^{2}\cdot \mathrm {precision} +\mathrm {recall} }}}$$

Two other commonly used ${\displaystyle F}$ measures are the ${\displaystyle F_{2}}$ measure, which weights recall higher than precision, and the ${\displaystyle F_{0.5}}$ measure, which puts more emphasis on precision than recall.

The F-measure was derived by van Rijsbergen (1979) so that ${\displaystyle F_{\beta }}$ "measures the effectiveness of retrieval with respect to a user who attaches ${\displaystyle \beta }$ times as much importance to recall as precision". It is based on van Rijsbergen's effectiveness measure ${\displaystyle E_{\alpha }=1-{\frac {1}{{\frac {\alpha }{P}}+{\frac {1-\alpha }{R}}}}}$, the second term being the weighted harmonic mean of precision and recall with weights ${\displaystyle (\alpha ,1-\alpha )}$. Their relationship is ${\displaystyle F_{\beta }=1-E_{\alpha }}$ where ${\displaystyle \alpha ={\frac {1}{1+\beta ^{2}}}}$.

Limitations as goals

There are other parameters and strategies for performance metric of information retrieval system, such as the area under the ROC curve (AUC).

See also

• Uncertainty coefficient, also called proficiency
• Sensitivity and specificity
• Confusion matrix

External links

• Information Retrieval – C. J. van Rijsbergen 1979
• Computing Precision and Recall for a Multi-class Classification Problem